Factors Influencing Gemstone Brilliance:
Many factors come together to determine the brilliance of a gem. However, its refractive index plays the most important role. And it is the light that exits the stone that predominantly determines its brilliance.
The outgoing light can behave in two ways:
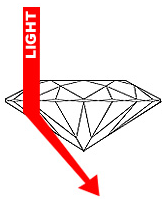
| 1 | It can leak out of the gem escaping from the bottom pavilion facets. In this case the departing light rays are not able to come back and meet the observing eye. Consequently, the gem looks listless and dull. It is less brilliant. |
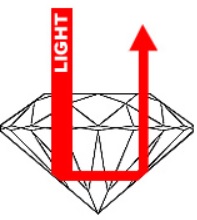
| 2 | The light can be completely reflected back into the stone. Here, the bottom pavilion facets act as highly polished mirrors. They reflect the light back through the top table and crown into the viewing eye. Evidently, the stone appears bright and vivacious. It is highly brilliant. |
What influences the travel of the light. Three things:
| A | The angle at which it is incident on the facet. It is called the angle of incidence. |
| B | The refractive index of the gemstone. |
| C | Proportions of the cut in correlation to the refractive index. |
A) Angle Of Incidence:
Imagine holding in your hand an exceptionally brilliant stone at an optimum viewing angle. At this angle of viewing, mirror-like facets reflect virtually all incident light back into the viewing eye and the stone appears absolutely brilliant. This is known as face-up brightness.
However, changing the tilt changes the angle of incidence which is no longer optimal. Total internal reflection flounders. Some of the light is able to seep and escape from the rear facets. As a result, the background of the stone becomes visible through these facets. Brilliance gets impacted. This is known as tilt-brightness and the phenomena is known as windowing.
With a gemstone of high refractive index (RI), you have to tilt to a greater degree for windowing to occur. Whereas in a gem of low RI, the window crops up even with a slight tilt. As such higher RI gems bounce and reflect light from wider angles. Therefore, they appear vibrant over wide-ranging orientations.
B) Role of Refractive Index:
In order to grasp the role of the refractive index, let us first understand what is refractive index (expressed as RI).
When light enters from a rarer medium (air) into a denser medium (our gemstone) it bends in one direction. Similarly, when light exits the gemstone and enters air it bends in the opposite direction. This bending is termed as refraction.
Even so, if the incident ray is perpendicular to the surface of the gem, bending of light (refraction) does not occur. It only occurs when this ray enters the gem at an angle. This angle is known as angle of incidence.
Thus refraction not only depends on the refractive index of medium but also on angle of incidence.
This angle of incidence is measured by imagining a straight line perpendicular to the surface of the gem. Further, this imaginary straight line is envisioned to penetrate the gem and continue in the same straight path inside the gem. This line is called the ‘normal’.
The angle that the incident ray of light makes with this normal is the angle of incidence.
The angle that the refracted ray of light inside the gem makes with this normal is the angle of refraction.
Both angles are different because of the bending of light ray.
Refractive Index is then calculated using the following optical physics formula:
R.I.= sin (angle of incidence) / sin (angle of refraction)
We have discussed that angle of refraction changes with angle of incidence. But this ratio sin i/sin r which is the refractive index always remains constant.
We have to understand two more concepts of physics & optics to learn how refractive index influences brilliance.
Critical Angle:
Above, we deliberated on one aspect of refractive index. We saw how light bends as it enters a gemstone. But brilliance is a function of how light exits a gem.
You see, a lot of light goes into the stone. But what we become aware of is the light that comes back out of the gem and reaches the eye. That’s relevant to the topic of our discussion.
And, Light about to leave a gem can behave in two ways.
First Way That Light Can Behave:
It can leak out and escape into the air by getting refracted away from the normal. In this case, the gem appears dull and listless. It is less brilliant.
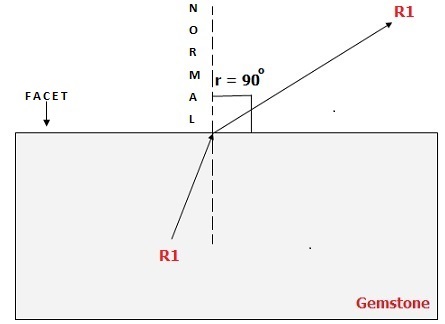
Also, this light escapes at different angles depending on the angle at which it strikes the facet in the gem. If it is perpendicular to the facet, it escapes without getting refracted. If you visualize the normal in the diagram below to be this ray, you get the picture of such a perpendicular ray of light.
Factors Influencing Gemstone Brilliance
Visualize ray R1 in the above diagram. It strikes the facet at an angle, gets refracted away from the normal and exits the gemstone.
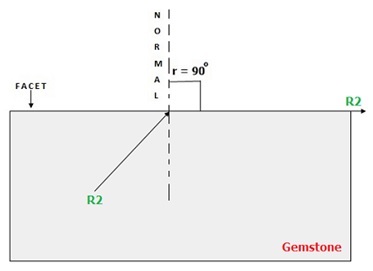
It is evident that there exists a particular angle of incidence when exiting ray will bend in such a manner that it comes out parallel to the facet. In the figure below, ray R2 is such a ray.
Factors Influencing Gemstone Brilliance
This angle exists in all transparent minerals and is known as the critical angle denoted by C.A. This angle can be calculated using the following formula:
Sin C.A. = 1/Refractive Index OR R.I.
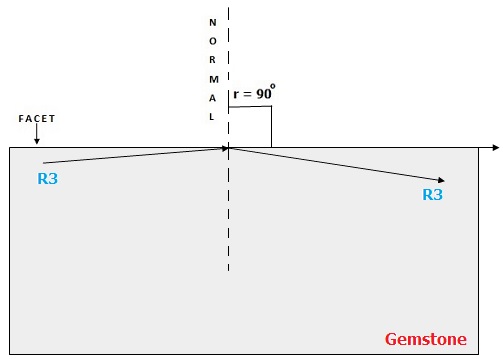
Second Way That Light Can Behave:
Factors Influencing Gemstone Brilliance
Moving further, (as seen in above diagram) when a ray of light happens to hit the facet at an angle greater than the critical angle, it shall not escape. Rather, it will be reflected back into the gem. This ray scores multiple reflections in the gem. Ultimately, it hits a facet at a particular precise angle. When this happens it finally exits the gem from the table and crown facets at the top of the gem and meets the observing eye. Such rays impart brilliance to the stone making it sparkle.
Angles of incidence, angles of refraction and the critical angle are all measured in reference to the normal.
Since the gem is a three dimensional object, the critical angle defines a conical shape in the gem. The opening angle of this cone is equal to the critical angle. This cone is centered on a normal to a facet. It is known as the cone of acceptance.
All rays of light unfortunate enough to strike the facet at angles within the cone will be reflected out of the gem without contributing to brilliance.
On the other hand, light-rays striking outside this cone will be reflected in a manner to stay within the gemstone. Subsequently, these rays, after numerous reflections, exit from the table and crown facets to meet the eye and contribute to brilliance.
The equation: Sin C.A. (i.e. Critical Angle) = 1 / Refractive Index tells us that refractive index and critical angle are inversely related. Higher the refractive index, lower is the critical angle leading to a narrower cone of acceptance. Because of this reason, a gem with a higher refractive index allows more rays of light to refract and bounce within the gemstone. Hence, higher refractive index leads to greater brilliance.
Remember, at the beginning of this article, we recorded that proportions of the cut in correlation to the refractive index is also one of the factors influencing gemstone brilliance.
In real life situations, incident rays of light arrive on the gemstone from all angles. It is impossible to assess all possible paths these rays will follow.
As such, several trigonometric calculations, adjustments and compromises are made while deciding the cut. Skilled gem-cutters then decide upon the cut after taking into consideration a number of factors like quality and size of rough, refractive index and concomitant critical angle. A cut drawing upon these factors produces the sparkle that we all love so much.
So cut is the most important C among the four Cs of diamond. A poor cut can mar the brilliance and beauty of the best of gemstones. An excellent cut can breathe life in lesser ones.
That concludes our article on Factors Influencing Gemstone Brilliance.